Kareköklü sayılar, bir sayının karekökünün tam sayı olmayan sonucudur. Örneğin, 16’nın karekökü 4’tür çünkü 4 x 4 = 16, ancak 17’nin karekökü tam sayı değildir.
Kareköklü sayılar, matematikte birçok farklı alanda kullanılır. Örneğin, trigonometrik fonksiyonların değerlerini hesaplamak, geometrik şekillerin alan ve çevrelerini hesaplamak, elektrik devrelerinde akım ve voltaj hesaplamaları gibi birçok uygulama alanı vardır.
Kareköklü sayılar pozitif veya negatif olabilir. Örneğin, -16’nın karekökü 4i’dir. Burada i, karmaşık sayılar alanında kullanılan bir sabittir.
Kareköklü sayıların işaretleri, özellikle matematiksel işlemler yaparken önemlidir. Örneğin, iki kareköklü sayının çarpımı, kareköklerin altındaki sayıların çarpımına eşit olur.
Ancak, farklı işaretli iki kareköklü sayının çarpımı bir karmaşık sayıya eşit olabilir.
Kareköklü sayılar, sıklıkla cebirsel ifadelerde kullanılır. Örneğin, (a + b)² ifadesi, a² + 2ab + b² olarak yazılabilir. Bu ifadeyi kareköklü sayılarla yazmak için, karekök içinde (a + b)² ifadesini yazabiliriz.
Kareköklü Sayılar
Kareköklü sayılar konusu, her sene sınavda sorusu olan önemli konulardan bir tanesidir. Kareköklü sayılar konusunu iyi öğrenmeniz halinde asla soru kaçırmayacaksınız. İsterseniz başlayalım.
Karekök alma, verilen sayının hangi sayının karesi olduğunu bulma işlemidir. (Negatif bir sayının karekökü olmaz. Çünkü hiçbir sayının karesi negatif değildir). Dolayısıyla bu sembol pozitif bir sayının karekökünü bulmak için kullanılır.
Tam Kare Sayılar
Bir tam sayının karesi olan sayılara “tam kare sayılar” denir.
Örneğin; 2.2= 4 olduğuna göre 4 sayısı bir tam kare sayıdır.
11.11=121 olduğuna göre 121 sayısı bir tam kare sayıdır.
Bunlardan yola çıkarak 0,1,4,9,16,25,36,49,64,81,100 sayılarının da tam kare olduğu görülmektedir.
| 12=1 | 62=36 | 112=121 | 162=256 |
| 22=4 | 72=49 | 122=144 | 172=289 |
| 32=9 | 82=64 | 132=169 | 182=324 |
| 42=16 | 92=81 | 142=196 | 192=361 |
| 52=25 | 102=100 | 152=225 | 202=400 |
- Tam kare sayılara karesel sayılar da denir. “0” için özel bir durum söz konusudur. “0” tam kare bir sayıdır fakat karesel bir sayı değildir.
*Karesel sayıların karekökleri de tam sayıdır.
Karekök alma işlemine değinmiştik,şimdi ise tam kare sayılarda uygulamasına bakalım;
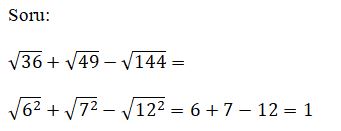
Şimdi ise tam kare olmayan sayıların karekök değerlerini hesaplamaya geçelim.
- Tam kare olmayan bir sayının karekök alma işlemini yaparkeno sayıya en yakın tam kare sayılardan yararlanılır. Öncelikle hangi iki tam kare sayı arasında olduğu bulunur. Daha sonra ise hangi tam sayıya daha yakın olduğuna bakılarak yaklaşık bir değer tahmin edilir.
Tam Kare Olmayan Sayıları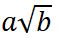 
şeklinde yazma
Özetle tam kare olan ifadeler kök dışına çıkarken, tam kare olmayanlar ise kökün içinde kalırlar.
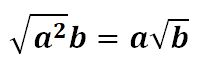
Peki bu işlemi nasıl yaparız? Gelin birlikte bakalım.
- Karekök dışındaki sayıyı karekökün içine alırken ise; karekök dışındaki sayının karesi alınarak kök içine yazılır ve varsa kök içindeki sayıyla çarpılır.
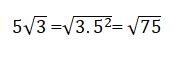
Kareköklü Sayılarda Sıralama
Kareköklü sayıları sıralamak oldukça basit bir işlemdir. Sıralama için verilen tüm sayılar karekök içine alınır ve kökün içindeki sayılar büyüklüklerine göre sıralanır.
• Negatif kareköklü sayılar sıralanırken aynı işlemler yapılır. Pozitif sayı gibi sıralanır ve sonra sıralanan sayılar arasındaki işaret tam ters yöne çevrilir.
Kareköklü sayılarda kökün dışına çıkarmayı da öğrendiğimize göre sıra işlemlere geldi sevgili gençler. Sırasıyla kareköklü sayılarda çarpma, bölme, toplama ve çıkarmayı inceleyeceğiz.
Kareköklü Sayılarda Çarpma İşlemi
Oldukça basit bu çarpma işlemi yapılırken; karekök dışındaki sayılar kök dışında çarpılır, karekök içindeki sayılar kök içinde çarpılır ve kök içine yazılır. Karekök içinde tam kare sayı varsa kök dışına çıkarılır.
Kareköklü Sayılarda Bölme İşlemi
Kareköklü sayılarda bölme işlemi, çarpma işlemi kadar basit bir işlemdir. Kareköklü sayılarda bölme yaparken karekökün dışındaki sayılar kendi arasında, karekökün içindeki sayılar kendi aralarında bölünür. Eğer karekök içinde tam kare bir ifade varsa kök dışına çıkarılır.
Kareköklü Sayılarda Toplama ve Çıkarma İşlemi
Kareköklü sayılarda toplama ve çıkarma işlemi yapmak için; karekök içindeki sayılar eşit olmak zorundadır. Karekök içindeki sayılar eşit değilse eşitlenir ve karekökün dışındaki kat sayılar arasında toplama çıkarma yapılır. Ortak karekök sonuca çarpan şeklinde yazılır.
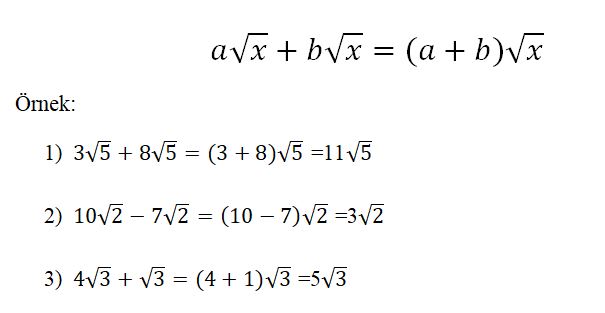
Kareköklü İfadeyi Doğal Sayı Yapma
Kareköklü bir ifadeyi doğal sayı yapabilmek için karekökün içindeki sayının tam kare bir sayı olması gerekmektedir.
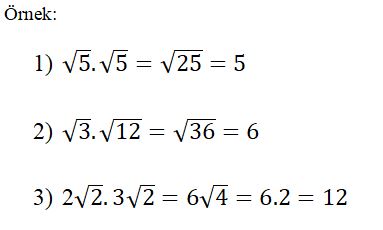
Not: Bir rasyonel sayının paydası kareköklü bir sayı ise; paydası doğal sayı yapılırken tam kare olacak şekilde payda genişletilir.
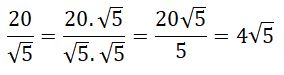
Ondalık Gösterimlerin Kareköklerini Hesaplama
Ondalık gösterimlerin karekökleri hesaplanırken, rasyonel biçimde yazarak pay ve payda kısımlarının ayrı ayrı kareköklerini hesaplayabiliriz.
Örnek:
Sonuç olarak, kareköklü sayılar matematikte önemli bir kavramdır ve birçok farklı alanda kullanılırlar. Bu sayıların işaretleri ve matematiksel işlemlerle ilgili kurallarını anlamak, matematiksel problemleri çözmek için önemlidir.